Архитектура — застывшая музыка. Это избитое выражение, приписываемое немецкому философу и теоретику искусства Фридриху Шеллингу, касается «большой» архитектуры. Однако с середины XX века художники все больше тяготеют к особым «малым» архитектурным формам — кинетическим скульптурам, которые застывшими назвать уже нельзя. Напротив, эти скульптуры, отдельные элементы которых, взаимодействуя, перемещаются по причудливым траекториям, завораживают зрителя постоянным движением. О кинетических скульптурах пишут книги искусствоведы, спорят посетители выставок. Совместно с Музеем современного искусства «Гараж» мы попытаемся взглянуть на них под другим углом — глазами математика.
С 17 марта по 9 мая в Музее современного искусства «Гараж» проходит «Трансатлантическая альтернатива» — первая в России крупная выставка, посвященная кинетическому и оптическому искусству Восточной Европы и Латинской Америки. На ней экспонируется более сотни произведений искусства 1950–1970-х годов, в том числе кинетические скульптуры, картины, рисунки, видео и инсталляции, а также уникальные архивные материалы. Логическим продолжением выставки «Трансатлантическая альтернатива» будет открытие «Атома» Вячеслава Колейчука — реконструкции монументальной цветодинамической скульптуры, стоявшей у истоков кинетического искусства в России. Мы решили разобраться, как устроен «Атом» и другие кинетические скульптуры.
Александр Колдер (Alexander Calder)
Американский скульптор (1898–1976), в начале 1930-х годов обратился к изготовлению динамических конструкций — так называемых «мобилей». Первые «мобили» Колдера приводились в движение моторами, но впоследствии, стремясь к созданию динамических систем, способных отражать постоянную изменчивость природы, Колдер перешел к «естественным» способам динамизации формы, а именно к конструкциям с неустойчивым равновесием, способным приходить в движение от малейшего колебания воздуха.
В своих работах Колдер использовал механизмы на основе рычажных весов — вращающиеся под действием потоков воздуха конструкции из проволоки и металла. К созданию таких «мобилей» применить классическую механику и математику довольно сложно, поскольку каждый из них состоит из большого числа частей совершенно разной формы. Скорее всего, параметры элементов скульптур — плоских грузиков разнообразной формы, расположенных иерархически, — определялись опытным путем, поскольку первую свою скульптуру Александр Колдер построил еще в 1930-х годах. Кстати, многие историки искусства считают, что он был первым, кто определил контуры «мобильного» направления кинетического искусства.
Впрочем, в настоящее время для разработки подобных конструкций можно использовать компьютер и метод конечных элементов, когда виртуальную модель разбивают на отдельные очень маленькие элементы, к которым применяют известные простые физико-математические законы и правила — правило равновесия рычага, правило нахождения центра тяжести плоской фигуры и так далее. Например, центр тяжести кольцевого сектора, который встречается в работах Колдера, рассчитывается по следующей формуле:
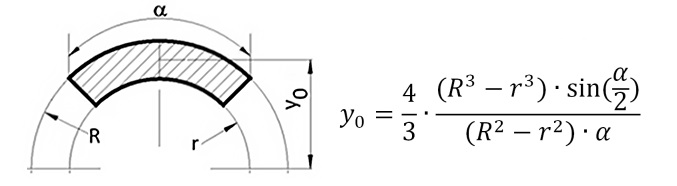
Часто повторяющийся у Колдера мотив — сложно устроенные и вложенные друг в друга «весы». Мобили, построенные по этому принципу, породили множество подражаний, а в интернете даже появляются инструкции, как сделать такой мобиль своими руками, без привлечения сложных вычислений:
Тео Янсен (Theo Jansen)
Нидерландский художник (родился в 1948 году), известен своими «искусственными формами жизни» — скелетообразными фигурами, способными передвигаться по песчаным пляжам под воздействием силы ветра. Генетические алгоритмы Янсена способны симулировать биологическую эволюцию видов.
В работах Тео Янсена находят применение идеи стопоходящей машины, основной узел которой переводит вращательное движение в поступательное. Скульптуры Янсена напоминают причудливые существа, которые ловко перебирают десятками ног и с легкостью движутся под действием ветра. Сам художник называет их «пляжными зверями», Strandbeest. Однако в действительности научить «зверей» ходить не спотыкаясь не так-то просто — необходимо не только корректно спроектировать каждую ногу, но и организовать их совместную работу. Для этого скульптору нужно решить систему нелинейных алгебраических уравнений, вытекающих из теоремы Пифагора.
Вот конкретный пример. Рассмотрим два рычага 1 и 2, соединенных шарниром в точке 5. Допустим, нам известны координаты концов 3 и 4 и мы хотим найти положение шарнира. Для решения этой задачи необходимо аналитически или численно решить систему двух нелинейных алгебраических уравнений, где L1 и L2 — это гипотенузы двух прямоугольных треугольников (длины рычагов), а x4 − x5, y4 − y5, x3 − y5 и y3 − y5 — это длины катетов. Как известно, эти величины связывает между собой теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
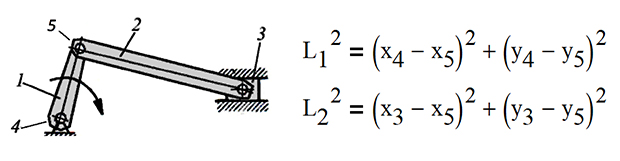
Разумеется, каждая «нога» содержит больше двух шарниров, а потому задача, которую предстоит решить художнику перед постройкой скульптуры, гораздо сложнее. Так или иначе, она сводится к оптимизации узлов — то есть подбору таких длин рычагов, при которых конструкция будет двигаться плавно, без толчков. Наконец, после того как скульптура будет спроектирована, необходимо сделать оптимизационные прочностные расчеты и убедиться в том, что она не сломается. Тут пригодятся знания, которые аккумулирует легендарная наука под названием сопротивление материалов (или, как ее сокращенно называют студенты, «сопромат»). И только после проведения всех расчетов скульптор может браться за инструменты, чтобы собрать конструкцию из пластиковых трубочек, деревянных брусков, скотча и полиэтилена.
Кстати, первым человеком, который стал применять высшую математику для проектирования подобных конструкций, был наш соотечественник Пафнутий Чебышёв, стопоходящая машина которого получила золотую медаль на Всемирной выставке в Париже в 1878 году и сейчас хранится в Политехническом музее в Москве. Впрочем, механические «звери» Тео Янсена ушли гораздо дальше — они запасают энергию ветра, надувая упругий «желудок», состоящий из пластиковых бутылок, умеют определять тип почвы, по которой ходят, и выбрасывают якоря, если ветер дует слишком сильно. Все это удается им без привлечения сложной электроники.
Лимэн Уитакер (Lyman Whitaker)
Американский художник, чья творческая биография насчитывает уже более пятидесяти лет. Последние тридцать лет он посвящает свои усилия «ветряным скульптурам» (Wind Sculptures).
Тогда как «мобили» Александра Колдера нужно демонстрировать в закрытом помещении, работы Лимэна Уитакера требуют дуновения ветра, от которого они начинают вращаться и создавать нужный «эстетический» эффект. В его работах используются законы аэродинамики, а сами скульптуры представляют собой своеобразные приборы для замера скорости ветра (анемометры, ветромеры).
Скорее всего, на создание мобилей Уитакера натолкнуло вращение традиционного флюгера с анемометром в виде четырех полусфер, которые используют метеорологи. Впрочем, сам автор утверждает, что черпает вдохновение в природе — в раскачивании травы и деревьев под действием ветра. Современные компьютерные программы позволяют моделировать геометрию обтекания газом или жидкостью сложных статичных или подвижных конструкций, однако Уитакер работает «по наитию», определяя профили каждого из «мельничных крыльев» опытным путем.
Обтекание тела воздухом описывается законом сохранения энергии — потенциальная энергия переходит в кинетическую и обратно, но сумма энергий остается постоянной. В газодинамике потенциальная энергия определяется давлением потока, а кинетическая — скоростью потока. Вместе их связывает формула, открытая Даниилом Бернулли в начале XVIII века. На рисунке видно, что скорость потока воздуха над крылом выше скорости потока под крылом.
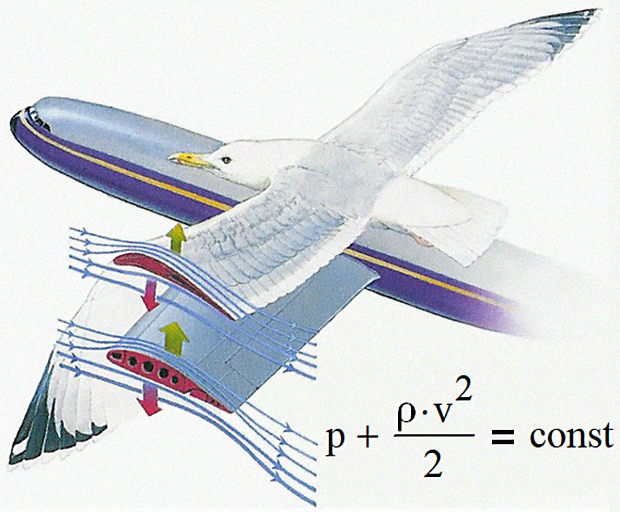
Перепад давлений под крылом и уравнение Бернулли
Следовательно, из-за эффекта Бернулли давление воздуха над крылом окажется ниже. Это и есть причина подъемной силы, заставляющей самолет и птицу держаться на воздухе, а кинетические скульптуры Лаимэна Уитакера — вращаться вокруг своей оси.
Франциско Инфанте-Арана (Francisco Infante-Arana)
Этот художник, сын испанского политэмигранта (родился в 1943 году в Саратовской области) и выпускник Строгановского училища, работал в СССР и России. В конце 1960-х годов начал выступать с инсталляциями под открытым небом, а в 1970 году стал создавать искусственные системы, аналогичные естественным явлениям (группа «Арго»).
Работы Франциско Инфанте-Араны пронизаны абстрактным геометризмом — например, его скульптура «Пространство-Движение-Бесконечность» напоминает вложенные друг в друга икосаэдры, пребывающие в непрерывном движении. Икосаэдр — это одно из пяти платоновых тел, то есть правильных многогранников. Напомним, что многогранник называется правильным, если он выпуклый, все его грани являются правильными многоугольниками, а в каждой вершине сходится одинаковое число ребер. В действительности, конечно, фигуры, образующие скульптуры Инфанте-Арана, не такие уж правильные, однако это не делает их менее интересными.
Легко показать, что в трехмерном пространстве правильных многогранников не может быть больше пяти — достаточно перебрать все возможные комбинации, для которых сумма углов одной вершины или одной грани будет меньше 360 градусов. Аналогичным образом можно получить, что в четырехмерном пространстве существует шесть правильных многогранников (один из них — широко известный тессеракт), а на плоскости их, очевидно, бесконечно много.
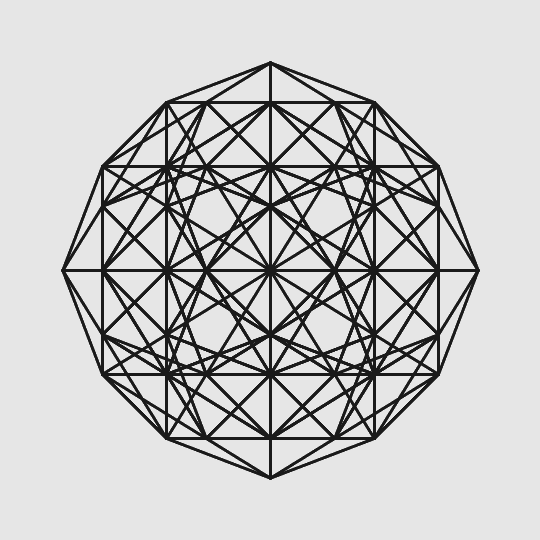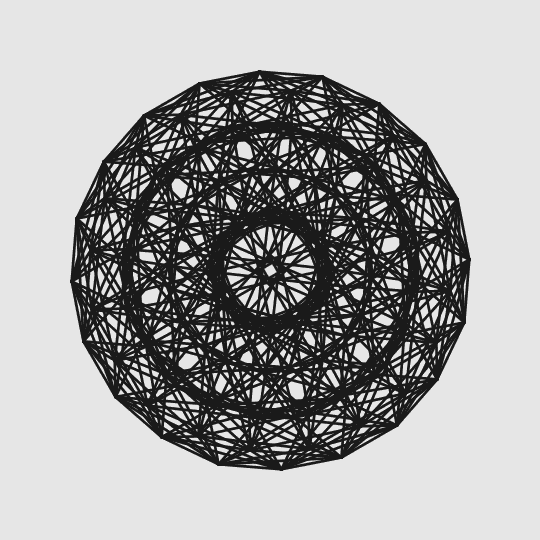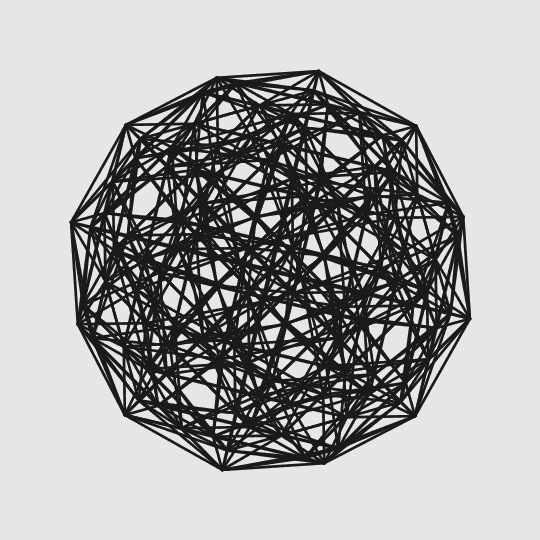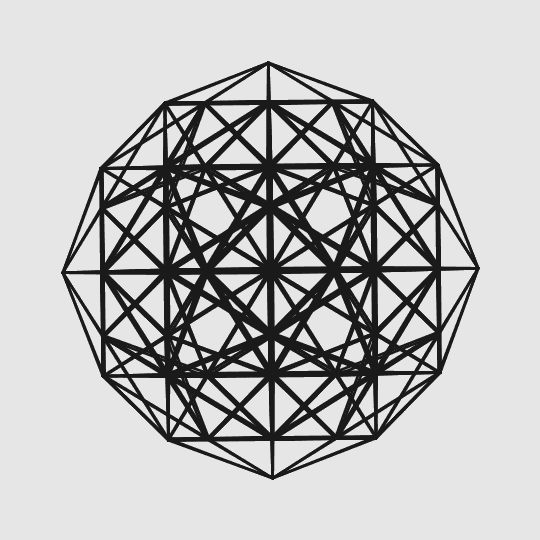
Проекция четырехмерного правильного шестисотячейника, гранями которого выступают правильные тетраэдры
alizar / geektimes.ru
Казалось бы, число правильных многогранников должно существенно зависеть от размерности пространства D. Однако в действительности в пространствах размерности больше четырех может существовать всего три правильных многогранника — правильный симплекс (пирамида), гиперкуб или гипероктаэдр. Вообще говоря, такая «универсальность» от размерности свойственна и для многих математических теорем — их утверждения легко обобщаются на случай D ≥ 4, но трехмерное пространство приходится рассматривать по отдельности.
Рубен Марголин (Reuben Margolin)
Американский художник, родившийся в 1970 году в Калифорнии, изучал монументальную живопись во Флоренции и Санкт-Петербурге, но впоследствии начал разрабатывать и собирать кинетические фигуры — главным образом из дерева.
Рубен Марголин дополнил механизмы Тео Янсена, базирующиеся на классической кинематике шарниров и рычагов, добавив к ним новые связи в виде… веревочек. С помощью таких механизмов также можно преобразовать вращательное движение в прямолинейное, однако с точки зрения математики их моделирование гораздо сложнее.
Так же, как и в «классических» стопоходящих машинах, здесь необходимо решать систему нелинейных алгебраических уравнений. Нелинейность возникает тут вследствие применения теоремы Пифагора (или теоремы косинусов) к двум шарнирно сопряженным рычагам, которые, как правило, и являются «элементарным атомом» многих кинетических скульптур. Если дополнительно используются и веревочки, то к рычагам и шарнирам прибавляются блоки в виде колесиков с желобками на ободе.
Если же нужно учитывать не только кинематику, но и динамику стопоходящей машины, то приходится решать и алгебраические, и дифференциальные уравнения, связывающие силу F с массой m и ускорением (второй закон Ньютона). А ускорение — это, как известно, вторая производная пути S от времени t: a = d2S/dt2.
Дифференциальные уравнения решать гораздо сложнее, чем алгебраические, сложнее и их численное моделирование. Например, в некоторых случаях небольшая ошибка в начальных данных ведет к существенному изменению траекторий системы — этот эффект известен как динамический хаос. Впрочем, для классических механических систем такое поведение было бы довольно неожиданным.
Вячеслав Колейчук
Вячеслав Фомич Колейчук родился в 1941 году в Московской области. Выпускник МАРХИ, в середине 1960-х годов был участником группы художников «Движение», позже создал собственную группу «Мир». На протяжении всей своей творческой деятельности Колейчук экспериментировал с разными видами визуальности — от кинетических фигур до физических моделей «невозможных объектов» в духе Роджера Пентроуза, оптических иллюзий и киноартефактов (знаменитая гравицапа из фильма Георгия Данелии «Кин-дза-дза»).

Вячеслав Колейчук и группа «Мир» — «Атом», светокинетическая установка (площадь Академика Курчатова, Москва,1967)
Фото: архив Вячеслава Колейчука
Первые свои кинетические скульптуры Вячеслав Колейчук создал еще в середине 1960-х годов. Так, в 1967 году, к 50-летию Октябрьской революции, на площади перед зданием Курчатовского института он построил светокинетическую композицию «Атом». В центре «Атома» находилась металлическая сфера, состоявшая из большого числа металлических трубок и удерживаемая благодаря самонапряжению железобетонных конструкций.
Чтобы рассчитать устойчивость подобной скульптуры, необходимо обращаться к науке о сопротивлении материалов, которую мы уже упоминали, когда говорили о «пляжных зверях» Тео Янсена. К сожалению, оригинальный «Атом» не сохранился, однако специально для Музея «Гараж» скульптура будет восстановлена под его руководством.
Впрочем, реконструированная композиция все-таки будет отличаться от оригинала — на этот раз ее будет сопровождать музыка, написанная композитором Николаем Хрустом для терменвокса и вокалоида.

«Невозможный треугольник», Вячеслав Колейчук
О художниках, работающих в области кинетического искусства, а также об их работах можно рассказывать бесконечно, но на этом мы решили остановиться и предлагаем вам пройти небольшой тест, который покажет, насколько вы разобрались с математической основой кинетических скульптур. А также еще раз приглашаем посетить выставку «Трансатлантическая альтернатива», на которой можно увидеть много других кинетических скульптур.
Кинетический тест
Отправьте нам запрос
Поиск на сайте
Наши клиенты и партнеры
Недавние публикации
- В скелете вымершего псового с патагонского погребения заподозрили останки питомца индейцев 16 апреля 2024
- Что нужно для развития в России технологий ИИ, обсудили на форуме «Открытые инновации» 16 апреля 2024
- На снимках солнечного затмения заметили огромное розовое пламя 15 апреля 2024
- Найден источник крупнейшей после Большого взрыва вспышки в космосе 12 апреля 2024
- Формирование визуомоторных ассоциаций оказалось зависимо от мозжечка 12 апреля 2024
